Vladan Majerech - NTIN061 Algoritmy a datové struktury II
Last Modified: 7.1.2018
Index
zápočtové příklady, odkazy, cvičení 1, cvičení 2, cvičení 3, cvičení 4, cvičení 5, cvičení 6, cvičení 7, cvičení 8, cvičení 9, cvičení 10, cvičení 11, cvičení 12, cvičení 13
Pro získání zápočtu z NTIN061 je potřeba získat (3/5 z možných bodů za domácí úkoly zadávané v průběhu semestru).
Zápočtové příklady
Pokud není uvedeno jinak, počet přidělených bodů rychle klesá v případě použití časově neoptimálních algoritmů. Za odevzdání po termínu je jen poloviční počet bodů. Termín je do počátku cvičení příslušného dne. Příklady s body uvedenými v závorce jsou bonusové, body je možno získat, ale nepočítají se do limitu požadovaných bodů.
| Kód | Body | Termín odevzdání | Zadání |
|---|---|---|---|
| rýmy | 8 | do 22.10. 9:00 | Interaktivní program nejprve ze vstupu načte slovník (množina přípustných slov) a pak začne dostávat dotazy, odpovědí na dotaz je jakékoli slovo, které má s dotazem nejdelší společný sufix (mezi slovy ze slovníku). Doba odpovědi by měla být nezávislá na velikosti slovníku, efektivita odpovědi je důležitější, než efektivita načtení slovníku. |
| podposloupnost | 12 | do 22.10. 9:00 | Spočtěte, kolikrát se daná jehla vyskytne v daném seně jako podposloupnost (možnost proložení jinými znaky). |
| cesty | 10 | do 29.10. 9:00 | Pro dané vrcholy $u$, $v$ v orientovaném grafu nalezněte maximální počet vrcholově disjunktních cest z $u$ do $v$. Můžete používat „známé“ algoritmy jako podprogramy. |
| věže a sloupy | 10 | do 5.11. 9:00 | Máme šachovnici $m\times n$ a na některých políčkách stojí sloupy. Na políčka (bez sloupů) je možno umísťovat věže. Každá věž ohrožuje políčka ve stejné řadě a stejném sloupci, ale pouze k nejbližšímu sloupu v daném směru. Otázkou je, kolik věží je možno rozmístit tak, aby žádná nestála na políčku ohroženém jinou věží. No a na Vás je popsat, jak nalézt odpověď (opět můžete používat „známé“ algoritmy jako podprogramy). |
| indukce | (10) | do 12.11. 9:00 | Doplňte argument do indukce dokazující, že FordFulkersonův algoritmus (s orákulem) může vybírat cesty celou dobu tak, aby neposílal po nějaké hraně tok jedním směrem a později jej musel kompenzovat posláním nenulového toku po hraně zpět. Po vybrané cestě algoritmu vždy posílá největší možný tok (v aktuálně zbytkové síti). Pokud by to nešlo, nalezněte (pokud možno co nejmenší) síť ve které to nepůjde. |
| kluby | 10 | do 19.11. 9:00 | Na kolejích jsou různé kluby, koleják může být součástí libovolného počtu klubů. Jste postaveni před úlohu vybrat z každého klubu předsedu a místopředsedu a to tak, aby každý koleják byl vybrán za nejvýš jeden klub a pro něj do právě jedné funkce. |
| FourKaracuba | 10 | do 26.11. 9:00 | Karacubův algoritmus redukuje úlohu násobení $n$ ciferných čísel na 3 násobení čísel zhruba poloviční délky. Navrhněte, jak by šlo totéž redukovat na 7 násobení čísel zhruba čtvrtinové délky. Předpokládáme $O(n)$ sčítání na redukci. |
| FibBase | (15) | do 3.12. 9:00 | Fibonacciho číselná soustava je soustava, kde kladné číslo uvádíme ve tvaru $a_0F_0+a_1F_1+\cdots +a_kF_k$, kde $F_i$ je Fibonacciho posloupnost $1,1,2,3,\dots$. V normalizovaném tvaru pro každé $i$ platí $a_i\in\{0,1\}$, navíc $a_i+a_{i+1}\le 1$. Navrhněte co nejmělčí hradlovou síť, které dostane dvě normalizovaná kladná čísla ve Fibonacciho soustavě a vrací jejich součet v normalizovaném tvaru. |
| porovnání | 10 | do 10.12. 9:00 | Vytvořte co nejmělčí hradlovou síť, která pro n-bitová čísla $a$, $b$ vydá $1$ právě když $a\le b$. |
| increment | (10+2) | do 17.12. 9:00 | Navrhněte jak k operacím Insert, FindMin, DeleteMin, Decrement optimalizovaným na amortizované časy $O(1)$, $O(1)$, $O(\log n)$, $O(1)$ přidat operaci Increment, která zvětší (určeným způsobem) hodnotu klíče na který ukážeme. Chceme za podmínky zachování složitosti ostatních operací dosáhnout co nejlepšího (amortizovaného) času přidané operace. Jste schopni dokázat, že lépe to nepůjde? (Uměli byste to i tak, že odkaz na původní prvek bude stále na tento prvek odkazovat? ... +2) |
| Hamiltonovské cesty | 10 | do 7.1. 9:00 | Dokažte, že zjištění zda v grafu existuje Hamiltonovská cesta je NP-těžké, jak ve variantě neurčených koncových bodů cesty, tak i v případě, kdy jsou jeden či oba koncové vrcholy určeny (jak pro orientované, tak pro neorientované grafy). |
| Id studenta | celkem | rozpad bodů |
|---|---|---|
| A | 57 | rýmy(8), podposloupnost(9), cesty(10), věže a sloupy(10), kluby(10), porovnání(10) |
| B | 103 | rýmy(8), podposloupnost(12), cesty(10), věže a sloupy(10), indukce(10), kluby(10), FourKaracuba(9), FibBase(14), porovnání(10), increment(8+2) |
| C | 60 | rýmy(8), podposloupnost(12), cesty(10), věže a sloupy(10), kluby(10), FourKaracuba(10) |
| D | 56 | rýmy(8), podposloupnost(8), cesty(10), věže a sloupy(10), kluby(10), porovnání(10) |
| E | 57 | rýmy(8), podposloupnost(12), cesty(10), věže a sloupy(7), kluby(10), porovnání(10) |
| F | 60 | rýmy(8), podposloupnost(12), cesty(10), věže a sloupy(10), kluby(10), porovnání(10) |
| G | 49 | rýmy(8), podposloupnost(6), cesty(10), věže a sloupy(10), kluby(10), Hamiltonovské cesty(5) |
| H | 60 | rýmy(8), podposloupnost(12), cesty(10), věže a sloupy(10), kluby(10), porovnání(10) |
| I | 55 | podposloupnost(9), cesty(10), kluby(10), FourKaracuba(4), porovnání(10), incerment(10+2) |
| J | 50 | věže a sloupy(10), kluby(10), FourKaracuba(10), porovnání(10), Hamiltonovské cesty(10) |
Odkazy na obdobné stránky
Cvičení Jirky Švancary, Miloše Chromého, Michala Oplera, Mateje Lieskovského, Jakuba Pekárka a rozcestník Jana Hrice.
Cvičení 1
Na prvním cvičení jsme na tržnici datových struktur prodávali to, co jsme se naučili. Postupně jsme prodávali haldy (Fibonacci), avl/vyhledávací/intervalové stromy, hash tabulky, DFU, trie, skončili jsme u zásobníků, front a obusměrných spojáků (seznamy s inserty a delete na význačných místech). Vždy mne zajímal prvořadě interface (a jeho asymptotická složitost), teprve v případě stejného interface mne zajímalo zda má jedna struktura nějaké výhody před druhou. V případě intervalových stromů jsem doplnil dotaz na počet reprezentovaných bodů v intervalu, což se hodí pro optimalizaci vícerozměrných dotazů. Výhodou (a,b)-stromů bylo lepší chování z hlediska využití vyrovnávacích pamětí. AVL stromy mají oproti RB nepatrně lepší hloubku v nejhorším případě. RB stromy v implicitní reprezentaci barev umožňují O(1) velké aktualizace a proto mají asymptoticky méně prostorově náročné persistentní verze (běžně se ale s persistencí nepotkáme). Naznačil jsem, že existují i Splay stromy. Na konci jsem naznačil, exitenci dalších struktur, doporučil jsem vyhledat si na internetu efektivní datovou strukturu Top Trees a naznačil jsem existenci „neefektivních“ Metrických stromů (při dotazech na malá okolí mohou být výrazně lepší než lineární).
Cvičení 2
Na cvičení jsme se zabývali hledáním textu v textu (jehly(jehel) v kupce sena). Snažil jsem se naznačit, že mnohdy bývá užitečnější si předzpracovat seno (google; sufixové stromy ... snad se to ani nedalo nazvat náznak). Vzpomenul jsem plovoucí hash algoritmus Rabin-Karp a pak jsme se dostali k Knuth-Morris-Pratt algoritmu a k jeho zobecnění Aho-Corasick. Nedělali jsme žádné důkazy koreknosti, jen jsme nakreslili automat a pověděli jsme si jak jej zkonstruujeme (včetně informace nutné pro hlášení jehel tvořících sufix aktuálně reprezentovaného slova). KMP stačí pole indexů, AC potřebuje obecné odkazy, jinak je AC rozšířením KMP. Uvědomili jsme si, že hlášení všech nalezených slov by mohlo výrazně převyšovat ostatní čas, takže pro úlohu spočtení počtu podvýskytů jednotlivých slov je efektivnější spočíst počet „významných“ návštěv stavů automatu a ty pak pronásobit počtem stavu odpovídajících nálezů. Chvilku jsme se pozdrželi obecným povídáním o potenciálech při rozvádění alternativní analýzy složitosti Aho-Corasick algoritmu.
Cvičení 3
Na třetím cvičení jsme se zabývali maximalizací toků v sítích, dali jsme společně dohromady definici problému, snažili jsme se jej napasovat na problémy z praxe, a pak jsme se zabývali algoritmy jak problém řešit.
Algoritmus nalézt nějaký tok a buď zjistit, že je maximální, nebo ve zbytku najít tok, o který by bylo možno původní navýšit, byla navrhovaná varianta. Upozornil jsem na alternativní variantu, kdy naopak začneme s maximálním skorotokem a postupně zajišťujeme, aby se z něj stal tok. Ve chvíli, kdy se tak stane (zbavíme se přebytků ve vrcholech s tím, že něco může vytéct i zdrojem) máme maximální tok.
Algoritmus se zlepšující cestou (Ford Fulkerson) nebyl překvapením, algoritmus se skorotokem (Goldberg Tarjan) není tak přirozený protože si potřebuje pomoci s výškami vrcholů, které v zadání nikde nefigurují.
Hráli jsme si s tím, jak vybírat zlepšující cestu co nejefektivněji a snažili jsme se dospět k časové složitosti závisející na počtu vrcholů a hran, nikoli na kapacitách hran. Hledat cestu s největší minimální kapacitou byla zajímavá myšlenka. Místo toho jsem nás navigoval směrem k použití cest s minimálním možným počtem hran (Edmons-Karp) a ukázali jsme pro takový případ časový odhad běhu algoritmu. Následně jsme ukázali (Dinic), že pro stejně dlouhé cesty nemusíme průběžňě aktualizovat zbytkový graf a můžeme hledat cesty pouze ve vrstevnaté síti (podgrafu hran na cestách nejkratších cest). Časovou složitost výpočtu blokujícího toku ve vrstevnaté síti uměl Dinic $O(nm)$, čímž byla celková složitost vylepšena z $O(nm^2)$ na $O(n^2m)$. Já jsem místo toho naznačil, že při volbě vhodné datové struktury je možno počítat blokující tok ve vrstevnaté síti v čase $O(m\log n)$, čímž dostáváme celkově $O(mn\log n)$.
V posledních osmi minutách jsme diskutovali, jak to vypadá s Goldberg-Tarjan algoritmem a princip důkazu (potenciál pro odhad počtu nesaturovaných push jsme stihli vymyslet). Celkovou složitost jsme nedopočítali. Jak se projeví optimalizace volby vrcholu s přebytkem v rozboru složitosti nám také zůstane na příští cvičení.
Cvičení 4
Začali jsme diskusí o domácích úkolech, pokračovali jsme ukázkou jak může Ford-Fulkerson nekonečně bloudit s limitou menší než je optimální tok. Pak jsme se dostali k analýze Goldberg-Tarjan algoritmu, zopakovali jsme to, co zaznělo na konci minulé hodiny a vrhli jsme se na analýzu varianty, kde pracujeme s nejvyšším vrcholem s přebytkem. Najednou byl konec hodiny a nestihl zaznít argument s tím, jak potenciál zvyšují saturované push. Konstatoval jsem, že dohromady dostáváme odhad $O(mnK+mn^2/K)$ počtu nesaturovaných push, což při volbě $K=\sqrt n$ dává i odhad celkového času algoritmu $O(mn\sqrt n)$.
Cvičení 5
Nejprve jsem krátce (interaktivně) zopakoval (a doplnil součet nárůstů $\Phi$) časový rozbor Goldberg-Tarjan algoritmu pracujícím s přebytkem v nejvyšších vrcholech. Pak jsme začali řešit úlohy. První byly hranově disjunkní cesty mezi dvojicí vrcholů v orientovaném grafu. Druhý se zabýval modifikací Ford-Fulkersona, kdy bychom nezvažovali doplňování hran umožňujících snižovat aktuální tok hranou. Ukázali jsme, že žádná standardní heuristika by nalezení maximálního toku negarantovala. Pak jsme se zamysleli nad tím, zda pro každou síť existuje posloupnost cest, nevyužívající doplňované hrany, které kdyby Ford-Fulkersonův algoritmus vybral tak by maximální tok nalezl. No a nad touto úlohou jsme vydrželi přemýšlet až do konce hodiny.
Jsme spíš přesvědčeni, že taková posloupnost vždy existuje. Poslední formulace přes indukci přes všechny rozklady všech maximálních toků na posloupnosti cest generované posíláním maximální tokem přípustné zbytkové kapacity. Indukce přes pořadí první cesty, kde Ford-Fulkerson pošle cestou více, než je zbytková kapacita toku (Ukážeme, že můžeme po následujících cestách posílat menší toky na úkor zvětšení toku kritickou cestou. Funguje to? Můžeme tak získat jiný maximální tok, kde cestu můžeme naplnit dle Ford-Fulkersona.). Musíme ještě ukázat, že pro danou síť takovéto indukci stačí konečný počet kroků. Uvědomme si, že pro iracionální poměr kapacit hran mohou být mezi generovanými posloupnostmi cest i nekonečné posloupnosti.
Cvičení 6
I na toto cvičení bylo plánováno dělat jednoduché příklady, a stejně jako minulou hodinu to dopadlo jinak. Nejprve jsem oznámil, že domácí úkol indukce je nejspíš přehnaně těžký a nebudu jej tedy počítat do limitu požadovaných bodů. Přesto se nebráním přidělit za něj body, pokud jej někdo vyřeší.
Pak jsme řešili hranovou $k$-souvislost, spokojili jsme se s tím, že jsme úlohu převedli na hledání toků v $n^2$ sítích. Pak jsme řešili modifikaci domácího úkolu věže. To nás odvedlo na otázku toků v sítích s jednotkovými kapacitami a na hledání maximálních párování nejen v bipartitních grafech. Odbočku s maximálním párováním jsme dotáhli ke květinkovému algoritmu (nevrhli jsme se na optimalizaci pokračování při nalezení květinky, spokojili jsme se s $O(mn)$ složitostí na pokus o vylepšení párování). Než jsme se stihli vrhnout na odbočku s jednotkovými kapacitami hran, zazněla otázka, jak bychom řešili věže v 3D.
S věžemi v 3D jsme strávili spousty času s neúspěšnými pokusy o převod na toky v sítích. Jeden z alternativních převodů končil u hypergrafu, kde políčkům odpovídaly trojice. Cílem bylo najít co nejvíce vrcholově disjunktních trojic. Upozornil jsem na úzkou souvislost s NP-úplným problémem 3D párování. NP-úplnost nás ale čeká až ke konci semestru a stejně nám došel čas. (Přesná souvislost byla u toho hypergrafu. V důkazu NP-těžkosti 3D párování se využívá trojice hyperhran lišících se po dvou v jediném vrcholu. V našem hypergrafu ale mohou mít dvě hyperhrany společný nejvýš jeden vrchol (vrcholem sjednocení trojic lišících se v právě jedné souřadnici, hrana odpovídá oné trojici, je tvořena vrcholy kdy je pokaždé jiná souřadnice proměnná.) Nicméně v důkazu NP-úplnosti stačí, když dané hrany mají jeden vrchol společný.
Mám takový pocit, že mám důkaz NP-úplnosti varianty věží,
kde je normální ohrožování, ale jsou zakázány některé pozice věží kaňkami.
(Je potřeba modifikovat důkaz NP-těžkosti 3D párování tak,
že vycházíme z SAT a nejprve transformujeme všechny proměnné, takže máme instance proměnných a ekvivalence instancí proměnných. S takto velkým omezením na tvar formule již je převod možný.)
Vyjde kvádr rozměrů $2E\times 2E\times 2$,
kde $K$ je počet klauzulí SATu,
$E$ je celková délka klauzulí (počet „instancí proměnných“).
V řezech dle prvního rozměru jsou nejprve čtverce instancí proměnných bez kaněk, rozmístěné v různých hloubkách (jinde jsou kaňky ... na obrázku přítomnost červené resp. zelené v RGB).
Pak jsou řezy odpovídající $K\le E$ klauzulím
(kde jsou instance proměnných místo původních proměnných)
v třetí souřadnici rovné R
a řezy odpovídající dodatečným klauzulím zajišťujícím ekvivalenci instancí v třetí souřadnici rovné G
(kaňky jsou všude mimo hloubek odpovídajích vybraným literálům).
Předpokládáme, že každá proměnná byla v původní klauzuli aspoň dvakrát, jinak můžeme původní formuli zjednodušit.
A co odpovídá literálu?
V daném čtverci proměnné jsou dvě možnosti, jak umístit věže.
Volným sloupcům jedné možnosti říkejme $x_k$, v druhé $\neg x_k$.
Ptáme se, zda jde umístit $K+3E$ věží
(v průmětu ignorujícím druhou souřadnici je pouze $K+3E$ sloupců,
kde se vyskytuje políčko bez kaňky, z každého tedy musí být jedno vybráno).
Alternativou je zabrat každou klauzulí tolik sloupců,
kolik má proměnných a kromě prvního sloupce umožnit položení věže libovolně v rámci oblasti proměnných klauzule.
Pak se ptáme, zda je možno umístit $4E$ věží, tedy tolik, kolik je velikost obou menších průmětů.)
Pro úlohu s překážkama místo kaněk je pořadí v jednotlivých rozměrech příliš limitující a pochybuji, že se podaří NP-úplnost snadno dokázat. Jako zadání to ovšem jednodušeji než zadání s kaňkami nevypadá.
Cvičení 7
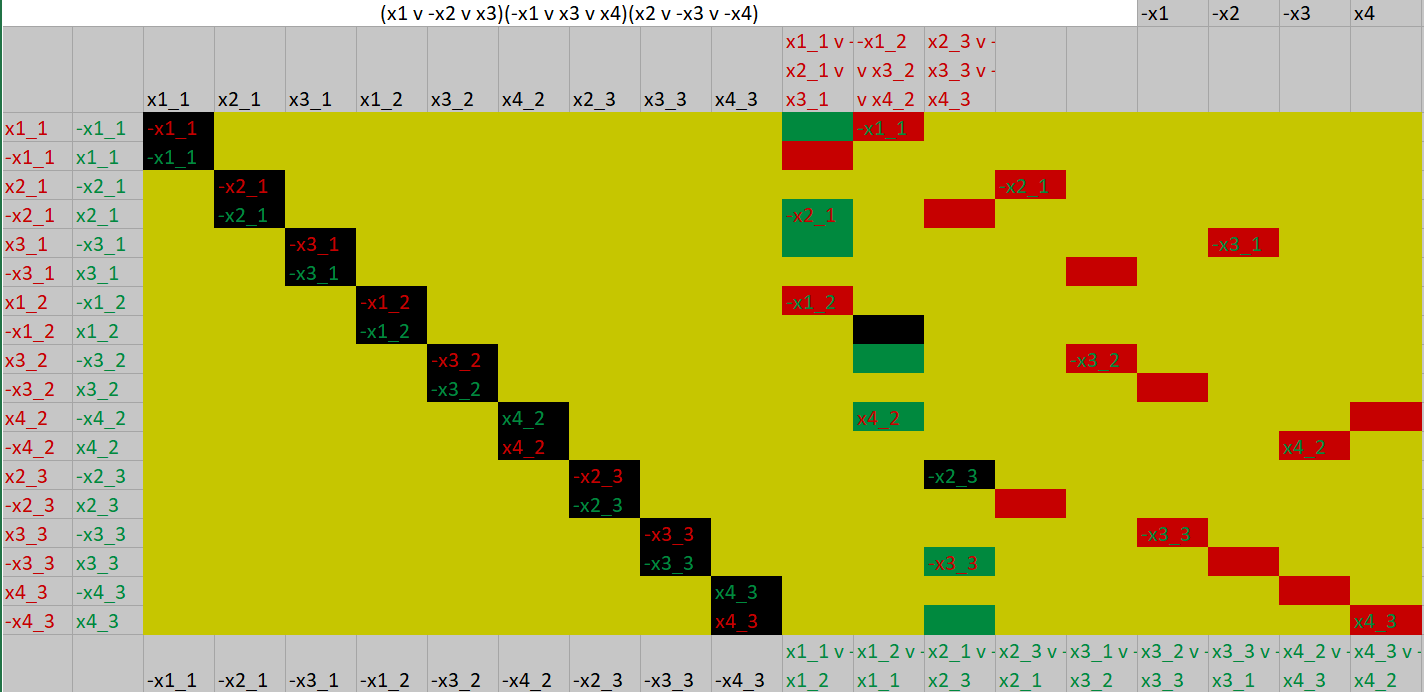
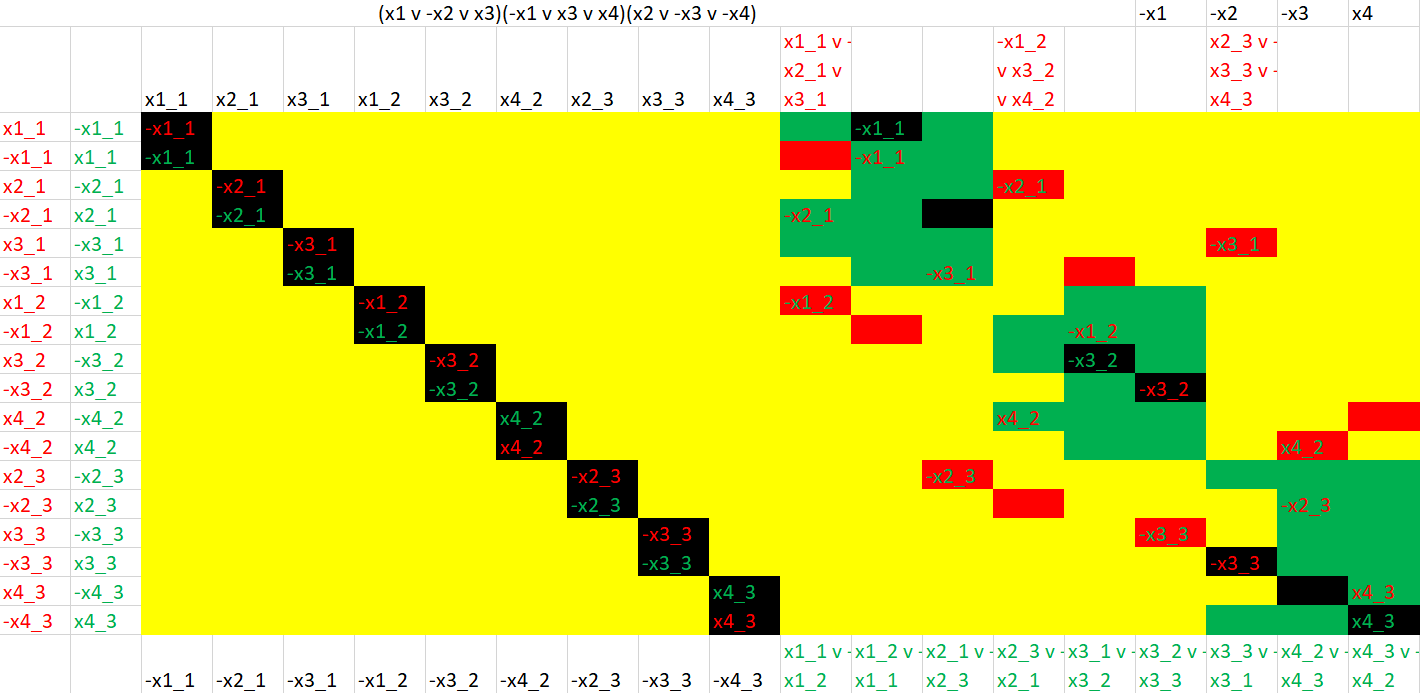
Celé cvičení jsme se věnovali Fourierově transformaci. Motivace byla násobení dlouhých čísel. Řešili jsme přes násobení polynomů, to přes převod z domény koeficientů do domény funkčních hodnot v šikovně vybraných bodech. $\omega=\sqrt[2^k]{1}$ (primitivní) se hodí, protože dosazování všech mocnin $\omega^j$ se dá paralelizovat (převést z násobení matic o plochách $2^{2k}$ a $\ell2^k$ na $\ell2^k$ operací a násobení matic o plochách $2^{2k-2}$ a $\ell2^k$.) s výsledkem dosazení $2^k$ hodnot v celkovém čase $O(k2^k)$. Inverzní transformace vypadá vpodstatě stejně, takže v tomto čase se dostaneme i z oboru hodnot do oboru koeficientů polynomů. Pokud mezitím po prvcích znásobíme (nebo provedeme jiné operace) v oboru hodnot, provede se nám totéž na výsledném polynomu. (Proč je součin transformačních matic pro $\omega$ a $\omega^{-1}$ vpodstatě jednotkovou maticí jsme zdůvodňovali, zmínil jsem se i o vztahu k MP3, jpg, jpeg2000, zpracování výrazně periodických signálů ... namotávání funkce na complexní válec, integrujeme průmět, pokud netrefíme periodu, signály mají těžiště blízko nuly. V skoro periodě dostáváme skoro statický obrázek na „osciloskopu“ a jeho těžiště typicky není v nule.)
Pak jsme se rozdělili na skupinky a prováděli jsme násobení malých polynomů buď v komplexních číslech $\omega=i=\sqrt[4]1$ nebo $\omega\equiv4\equiv\sqrt[4]1\,(\hbox{mod }17)$. Výsledky dopadly dle očekávání, občas i s paralelizací.
Cvičení 8
Na začátku hodiny jsme si řekli, co to jsou hradlové sítě a našli jsme univerzální binární hradlo nand. (Kromě obecné konstrukce jsme ukázali, jak pomocí něj (efektivně) vytvořit negaci, or a xor).
Pak jsme se věnovali DU indukce (přinejmenším osnova důkazu snad byla zřejmá). (V minimálním protipříkladu na FF* algoritmus nemůže existovat zlepšující FF* cesta pro žádný tok $T$ ... cesta kde je minimální kapacita hrany nejvýš tak velká jako maximální tok každou hranou. Z existence takové cesty by plynula existence menšího (počet hran) protipříkladu. Dále jsme ukázali (naznačili), že existence minimálního řezu $(A,B)$ „uvnitř“ grafu by znamenala existenci menšího protipříkladu. V jednom grafu nahradíme $A$ zdrojem, v druhém $B$ stokem. Oba grafy jsou menší a pokud v žádném není protipříklad, existuje zlepšující FF* cesta vůči nějakému maximálnímu toku. Pak jsme ukázali, že můžeme zvětšít kapacity hran zdrojového, případně i stokového řezu a nová síť bude stejně velký protipříklad (jinak by nám našla FF* zlepšující cestu v původní síti vůči nějakému jejímu maximálnímu toku). (Po nalezení maximálního toku (zvětšujícího maximální tok v původní síti) snížíme navýšené kapacity podle nalezeného toku tak, aby původní minimální řezy byly mezi minimálními řezy výsledné sítě. Kapacity budou aspoň tak velké jak původní.) V novém protipříkladu máme ale i jiný minimální řez. Ze sítě s pouze zdrojovým minimáním řezem tak dostáváme síť se zdrojovým i stokovým minimálním řezem. Ze sítě se zdrojovým i stokovým minimálním řezem dostáváme síť, kde exituje i další (nutně vnitřní) řez. Pak ale existuje i menší protipříklad a to je spor.)
Pak jsme se vrátili zpět k hradlovým sítím a přišli na to, jak sčítat dvě $n$-ciferná čísla sítí hloubky $O(\log n)$. Klíčovým bylo nalezení přenosů v hloubce $O(\log n)$. Závěrečný xor tří hodnot pro každou cifru již zvládneme v konstantní hloubce. Trikem k nalezení přenosu v malé hloubce je že výsledek součtu známých hodnot a neznámého přenosu je známá funkce neznámého přenosu (konstanty 0, 1 či kopie přenosu). Skládání takovýchto funkcí není problém a umožní nám to přenos v řádu $2^k$ v hloubce $k$ a všech řádů od $2^k$ do $2^{k+1}$ v dodatečné hloubce $k$.
Cvičení 9
Na devátém cvičení jsme se věnovali třídícím sítím. Nechť je pro jednoduchost $n$ mocninou dvojky. Začali jsme bitonickou třídící sítí, která umí setřídít bitonickou posloupnost v hloubce $\log_2 n$ a nesetříděnou posloupnost v hloubce $1+2+\cdots+\log_2 n\in O(\log^2n)$. V každé hloubce bylo $n/2$ komparátorů. (Vztah k sekvenčnímu algoritmu, efektivní implementace swapování přidává $O(\log n)$ overhead, takže utřídění bitonické posloupnosti vyžaduje $O(\log^2 n)$ času.)
Pak jsme se věnovali třídící síti založené na MergeSort. Ukázali jsme, že také potřebuje celkovou hloubku $1+2+\cdots+\log_2 n\in O(\log^2n)$, že houbka $\log_2n$ stačí na setřídění posloupnosti skládající se ze dvou utříděných posloupností stejné délky (u bitonického třídění mohly být délky různé). Na rozdíl od bitonického není potřeba $n/2$ komparátorů na každé patro. Plných je $\log_2 n$ pater, $(\log_2 n)-1$ pater je zaplněno jen z poloviny, $(\log_2 n)-2$ ze tří čtvrtin, $(\log_2 n)-k$ pater z $1-1/2^k$ tiny. Velikost obou sítí je $O(n\log^2n)$. (V případě implementace na $n/2$ jádrech může merge sort využít volného času procesorů.) Dokázali jsme korektnost obou sítí.
Cvičení 10
Na konci minulého cvičení jsme se dohodli, že dnes budou haldy. Ukázal jsem tedy odvození hald na základě principu extrémně drahého porovnávání. Nejprve jsem vyjmenovali zajímavé haldové operace. Postupně jsme přidávali operace, potenciály a invarianty, doplňovali detaily implementace. Začali jsme s rozborem dvojice Insert, FindMin se složitostmi $\bigl(O(1)$, $O(n)\bigr)$. Po zavedení $t_0\Phi_0$ jsme dostali ceny $\bigl(O(1), O(1)\bigr)$. Pak jsme přidali DeleteMin. Bez $t_0\Phi_0$ bychom měli $\bigl(O(1)$, $O(n)$, $O(1)\bigr)$, s $t_0\Phi_0$ pak $\bigl(O(1)$, $O(1)$, $O(n)\bigr)$. Lineární složitost se dá preventovat pokud zajistíme invariant $(c,q)$ úzkosti. Tím se nám zkomplikuje FindMin (musíme porovnávat stromy stejného řádu, pokud to jde). Dostaneme pak složitosti $\bigl(O(1)$, $O(\log n)$, $O(n)\bigr)$, ale s potenciálem $t_0\Phi_0+t_1\Phi_1$ pak $\bigl(O(1)$, $O(\log n)$, $O(\log n)\bigr)$. Rozšířením potenciálu $t_0\Phi_0+t_1\Phi_1+t_2\Phi_2$ přeorganizujeme ceny na $\bigl(O(1)$, $O(1)$, $O(\log n)\bigr)$ což nám pro Binomiální haldy vyhovuje. Složitost máme v nejméně často používané operaci a dostáváme $O(n\log n)$ pro řazení na základě porovnávání, což víme, že je optimum.
Následně přidáme Decrement. Triviální implementace vede k $\bigl(O(1)$, $O(1)$, $O(n), O(1)\bigr)$, protože se rozbije invariant $(c,q)$ úzkosti. Snižování řádů všem vrcholům na cestě ke kořeni vede k $\bigl(O(1)$, $O(1)$, $O(\log n), O(n)\bigr)$. Značkování kritických vrcholů a omezení aktualizace řádů jen na cestu dokud jsou vrcholy kritické (s odstraňování kritičnosti uvnitř cesty) vede také ke složitostem $\bigl(O(1)$, $O(1)$, $O(\log n), O(n)\bigr)$ s tím, že invariant úzkosti funguje pro jiná $c,q$. Vůči potenciálu $t_0\Phi_0+t_1\Phi_1+t_2\Phi_2+t_3\Phi_3$ dostáváme výsledné $\bigl(O(1)$, $O(1)$, $O(\log n), O(1)\bigr)$. Vzhledem k tomu, že nyní invariant úzkosti garantuje minimální velikost stromu řádu $k$ rovnou Fibonacciho číslu $F_k$, říká se těmto haldám Fibonacciho.
Nevýhodou Fibonacciho hald vůči Binomiálním je nutnost udržovat odkazy směrem ke kořeni a seznamy „sourozenců“ musí umožňovat odstraňování libovolného prvku v konstantním čase (dva odkazy místo jednoho). Navíc interface musí při vkládání prvku vracet odkaz, pomocí něhož může v budoucnu vnější svět na prvek ukazovat. Bezpracně dostáváme rozšíření o operaci Delete v ceně $O(\log n)$. V případě, kdy již s haldou nechceme pracovat, můžeme uvolnit paměť v čase (a ceně) $O(n)$, místo abychom plýtvali časem na posloupnost Delete(Min).
Algoritmicky netriviální je pouze operace FindMin, kde si musíme dát pozor, abychom v první fázi detekovali stromy stejných řádů efektivně, a abychom v přechodu do druhé fáze dostali seznam stromů efektivně (čas omezený počtem stromů).
Při snižování řádů si musíme dát pozor, abychom nevytvořili stromy záporného řádu (možnou variantou je při odznačování kritických vrcholů vytvářet další typ vrcholů a na novém typu ukončovat snižování řádů).
Ve zbylé čtvrthodině jsem pohovořil o možnosti ušetřit parent pointer. Důsledkem je, že Cut(součást Decrement) většinou nemá přístup k rodičům. Nemáme tedy šanci snižovat v takovém případě řády rodičům. Vzhledem k tomu, že největší potomci jsou na konci seznamu sourozenců a seznam můžeme místo nil ukončit odkazem na rodiče, tak v případě posledních dvou sourozenců můžeme přepočítání řádu propagovat do rodičů. Řád bude definován na základě řádu posledního a případně i předposledního sourozence (pokud se jejich nekritický řád liši nejvýš o 1). (Nekritický řád je definovaný při vzniku hrany v první fázi FindMin, řád může poklednout o 1, čímž se stane vrchol kritickým, kritický nesmí být poslední sourozenec, pokud by předposlední sourozenec neměl velký řád.) Za těchto předpokladů platí invariant $(c,q)$-úzkosti, s tím, že pro minimální velikost stromu řádu $k$ dostáváme rekurenci $M_k=M_{k-2}+M_{k-3}$, tedy stejnou, jako má Padovan posloupnost. Vyvažování řádů si vyžaduje zavedení tří dalších potenciálů. Potřebujeme udržovat největší garantované sourozence na konci seznamu, takže udržovat potomky neovlivňující řád na začátku seznamu. Findmin proto v první fázi přidává na konec a v druhé na začátek seznamu sourozenců. Pokud klesne řád nějakého potomka více než o 1 pod nekritický řád, je potřeba potomka přemístit před začátek potomků, kde řád dosud takto nepoklesl. (Potomky dělíme na vnější a vnitřní, pořadí vnějších je nepodstatné, vnitřní jsou seřazeni podle neklesajícího nekritického řádu.) Nemůžeme vnitřního potomka udělat vnějším a přemístit v době, kdy nemáme přístup k rodičovi. Tento přesun proto předplatíme (další potenciál) a odložíme na dobu, kdy se potomek ocitne mezi posledními dvěmi potomky (neumístěný vnější potomek). Pokles počtu vnitřních potomků, prodlouží budoucí přepočítávání řádů. Abychom toto přepočítávání udrželi amortizovaně konstantní, musíme přidat potenciál jakožto součet přes jednotlivé vrcholy rozdílů mezi řádem a počtem vnitřních vrcholů. (Řády nesnižujeme, ale přepočítáváme. Aktualizace končí, když nemáme přístup k rodičovi, nebo se řád přepočtem nezměnil. Řád může klesnout skokově, ale na to jsme si našetřili operacemi, které řád neovlivnily.) Posledním potřebným potenciálem je potenciál počítající počet vrcholů, jejichž řád je stejný jako řád největšího potomka (nebezpečné vrcholy). Amortizovaný rozbor se zjednoduší, pokud v první fázi operace FindMin odstraňujeme nebezpečné vrcholy (nejtěžšího potomka prohlásíme za vnějšího, dokud nám buď klesne řád na 0, nebo se nekritický řád posledních dvou potomků bude lišit o 1) na toto máme předplacený čas v potenciálech. (Garantuje nám to, že vnitřni vrcholy budou seřazeni podle (ostře) rostoucího nekritického řádu.)
Cvičení 11
Tématem cvičení byla NP-úplnost a převoditelnost. Nejprve jsem ukázal, že SAT je v NP a zárověň je NP-těžký, tedy je NP-úplný. (Polynomiální zřetězení podformulí $Next(\alpha_i,\alpha_{i+1})$ a počáteční a koncová podmínka).
Následně jsem ukázal typickou metodu na důkaz těžkosti jiných NP jazyků. Ukážeme, že v jazyku dokážeme zapsat boolovské proměnné a jejich negace, dokážeme, že jsme schopni v jazyku zachytit nezávisle jednotlivé klauzule SATu. Příkladem byl důkaz NP-těžkosti barvení grafu 3mi barvami. Deklarační trojúhelník na pojmenování barev, deklarační trojůhelníky sdílející nebooleovskou barvu deklarují vždy proměnnou a jejich negaci. Dva trojúhelníky spojené hranou a připojené hranami ke třem literálům a FALSE umožňují doobarvení, právě když ty čtyři vrcholy nemají stejnou barvu (ty 3 literály nejsou současně FALSE). Takto jsme schopni vytvořit klauzule. Pokud najdeme obarvení grafu, obarvení význačných vrcholů definuje pravdivost a při ní jsou všechny klauzule pravdivé. Naopak, pokud někdo nalezne ohodnocení proměnných, pro něž je formule pravdivá, můžeme podle něj obarvit příslušné vrcholy a i vrcholy podgrafů odpovídajících klauzulím bude možno doobarvit.
Dalším příkladem byl Plesníkův důkaz NP-těžkosti hledání Hamiltonovské kružnice v orientovaném grafu. Dokonce v bipartitním grafu s celkovým stupněm vrcholů 3, kde v jedné partitě je indegree 1 a v druhé outdegree 1. Jako bonus jsme slíbil to, že budeme umět graf udělat rovinný. Jako proměnná nyní sloužila rozbočka vložená na hranu, která určitě leží na HK. Pokračování jedním směrem znamená ohodnocení true, druhým směrem false. Ukázali jsme konstrukci pro nonekvivalentítko toho, zda po cestě od rozbočky HK vede. Následně jsme ukázali jak propojit kružnici reprezentující klauzuli s rozbočkami literálů klauzule. Pokud ani jeden z literálů nebude pravdivý, kružnice zůstanou izolované a nedostaneme Hamiltonovskou kružnici. Propojky byly navrženy tak, aby bylo z jakéhokoli pravdivého literálu možno odbočit do kružnice klauzule, aby z kružnice klauzule bylo možno projít odbočku nepravdivého literálu, a aby v případě dalšího pravdivého literálu bylo možno projít část vrcholů konstrukce z literálu a zbytek z kružnice klauzule. Pokud je formule splnitelná, určí nám splňující ohodnocení proměnných výběr v rozbočeních proměnných a tím i literálech klauzulí, konstrukce klauzulí umožňuje prvním pravdivým literálem kružnici klauzule s hlavní kružnicí propojit a ostatními literály kružnice nerozpojit. Pokud nalezneme Hamiltonovskou kružnici, rozbočky v oblasti proměnných nám definují ohodnocení proměnných a protože jsou kružnice klauzulí napojeny na HK, musí být pro toto ohodnocení klauzule pravdivé a tedy formule splněna.
Na dotaz, zda je možno zjednodušit konstrukci tak, aby nebylo potřeba posledního popsaného průchodu byla odpověď ANO, pokud bychom převáděli z „1 in 3 SATu“. Komplikuje se pak ale argumentace toho, že nemáme řešení kružnice, pokud je formule nesplnitelná (resp. nesplněná pro dané ohodnocení proměnných). Problém s kterým se musíme vypořádat, je případ 3 pravdivých literálů v klauzuli. Zůstane v takovém případě část kružnice klauzule oddělena od hlavní kružnice?
O „1 in 3 SATu“ jsme si ukázali, že je také NP-úplný. Zformulovat v něm garvení grafu 3-mi barvami bylo velice jednoduché. (Ani nevím, jak bych převod ze SAT dělal bez použití mezikroku s barvením.) (Vzhledem k tomu, že „1 in 3 SAT“ je možno formulovat jako speciální případ celočíselného lineárního programování, víme, že tento zobecněný problém je taky NP-úplný.)
Pak jsme si ještě pohráli se SAT a redukcí počtu výskytů proměnných. Čímž jsem vytvořil předpoklady k pochopení konstrukce úlohy s 3D neohrožujícími se věžemi.
Kromě toho jsme stihli vsuvku o převodu mezi orientovanými a neorientovanými Hamiltonovskými kružnicemi a důsledek na složitost rozhodování, kudy se má „had“ vydat, která v sobě hledání Hamiltonovské cesty v grafu se stupni vrcholů nejvýš 3 skrývá jako podproblém.
Cvičení 12
Pokračovali jsme v příkladech na převoditelnost dokazujících NP-úplnost. Začali jsme bervením grafů více než 3mi barvami. Pak jsme se zabývali rovinnou 3barevností. Následovaly kliky, nezávislé množiny a vrcholová pokrytí. Pak jsme se dostali k problému batohu. Skončili jsme s loupežníky.
Cvičení 13
Na posledním cvičení jsme si nadále hráli s $NP$-úplností. Nejprve jsme se krátce věnovali aproximacím, pak jsme přešli ke kachličkování ve všech variantách, jaké nás napadly. Klasické bez otáčení se strakatou koupelnou si zasloužilo důkaz převodem z TS. Pak jsme se věnovali odstranění strakatosti okraje koupelny (nemohli jsme ale zmenšit zadání udáním rozměru koupelny v poziční soustavě). Pak jsme se věnovali zadáním s možností otáčet či převracet kachlíky. Kartézský součin zadání s jednoznačně vydlážditelnou koupelnou to řešil. Zajímavé bylo, že při umožnění převracení s jednobarevnou koupelnou byla úloha NP těžká jen pro koupelny lichých rozměrů, které byly skoro čtvercové.
Další modifikací bylo, když místo katalogu byl dán seznam kachlíků (Eternity2). Ukázalo se, že to hezky souvisí s HK (na grafech malého stupně vrcholů).
Poslední modifikací bylo, když jsou kachlíky již umístěny na svých místech, zbývá je jen správně natočit. Tak již jsme neměli čas dokazovat $NP$-úplnost pořádně, jen jsem naznačil, jak vytvořit 1 in 3 SAT klauzule, literály a jak zajistit ekvivalenci leterálů. Na vše stačili kachlíky 4 druhů: 0,1,I a L.