Exercises 25. 3. 2021: (a,b)-trees and bit of splay trees
Ex. 1: Insert and delete
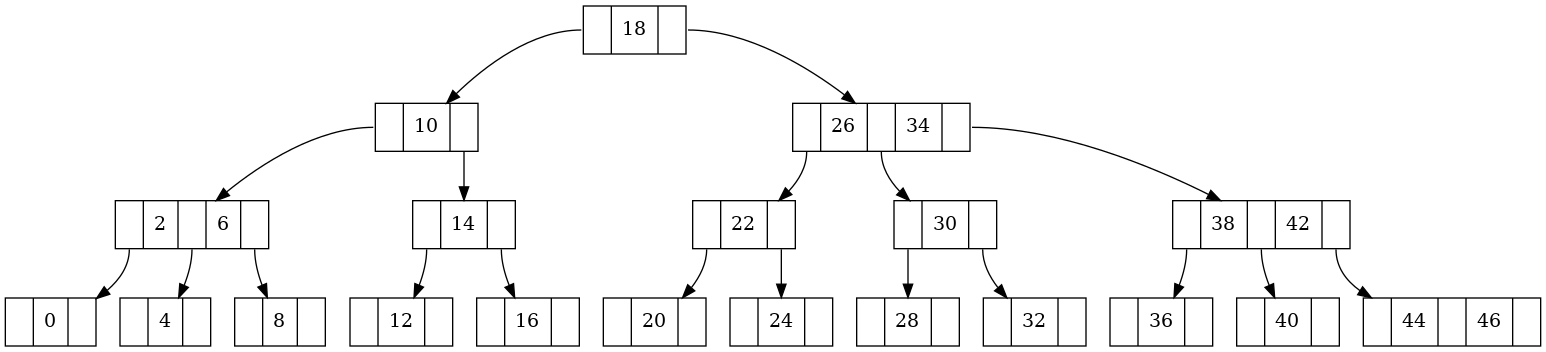
Perform following operations on the (2,3)-tree from the picture (perform each
operation separately):
- Insert 7
- Insert 48
- Delete 44
- Delete 40
- Delete 32
- Delete 30
- Delete 16
You can check you solution in a visualisation,
tree from the picture can be created by inserting following keys (in that order):
(the original sequence was wrong, this one should be correct)
28, 24, 26, 18, 0, 36, 16, 34, 22, 10, 2, 30, 4, 6, 20, 12, 32, 38, 14, 8, 40, 42, 44, 46
Note that visualisation only allows \((\lceil b/2 \rceil,b)\)-trees.
Ex. 2: Height of (a,b)-tree
Prove the bounds on the height of a (a,b)-tree from the lecture. That is, prove that
(a,b)-tree with \(n\) keys has height between \(\log_b (n+1)\) and \(1+\log_a
((n+1)/2)\). Note that height is measured in the number of edges, that is, a tree with
only a root and external nodes has height 1.
Hint: Go the other way around and calculate what is the maximum and minimum number of keys a tree of height
\( h\) can contain. This should give you the desired bounds on height.
Ex. 3: Naive splay (from previous practicals)
Proper splay trees use double rotations if possible. What happens if we implement
splay naively, using single rotations?
- Design a sequence of operations that creates a splay tree of linear depth, both
for proper splay trees and for naive splay trees. Hint: Inserts are enough. With
proper order, you can force even a proper splay tree to perform only single
rotations.
- Using the tree from previous task, desing sequence of \(k\) operations that has
total complexity \( \Omega(kn)\) in naive splay tree. What happens if we run the same
operation in a proper splay tree?
