Cvičení 27. 10. 2021: (a,b)-stromy
Úvodní povídání
Řešení splay_operation
- Vesměs všechny řešení byla v pořádku, pokud ne, tak typicky opomenutí nějakých
případů v remove (typicky když reálně mažu list).
- Vždy splayuju nejhlubší vrchol na který sáhnu! Plus mínus rodič/potomek,
důležité je, aby mi splay zaplatil z potenciálu potenciálně lineární cestu, kterou
jsem prošel.
- Při findu musím splayovat i když klíč nenajdu (na wiki je to v kódu špatně).
Taktéž pri insertu, když klíč už ve stromě je a analogicky při deletu.
- V remove bývá problém, když je třeba replacement null, tak je stejně třeba něco
splayovat. Co univerzálně funguje je prostě vysplayovat rodiče vrcholu, který reálně
smažeme (tj. v případě dvou synů to minumum z pravého podstromu).
Poznámky ke splay_experiment
- DŮLEŽITÉ! Pokud vaše řešení splay_operation nepoužívá metodu
rotate z
templatu, musíte kód experimentu/vaší implementace upravit tak, aby správně počítal
rotace. Běžně se to totiž dělá právě přes volání metody rotate
- Začněte vždy tím, že okomentujete, co vidíme v grafu, plus relevantní teorií.
Jinak se může stát, že vy v grafu vidíte \( \log(n) \), ale čtenář vidí \(\sqrt{n} \),
takže čtenáři zbytek textu nebude dávat smysl. Samozřejmě, detailně komentovat popisky
os nemusíte, od toho tam ty popisky os jsou.
- To, že po vás nechceme formální důkazy vašich tvrzení ještě neznamená, že můžete
tvrdit netriviální věci jako fakt jen tak bez argumentů. Pokud něco netriviálního
tvrdíte, tak to musíte podpořit nějakými argumenty. Nemusí být špatně argumentovat i
obrázkem.
- Důsledně rozlišujte mezi fakty (víme z přednášky, ...), pozorováními z naměřených
dat a hypotézami.
- Dejte si pozor, aby vám popisky nezakrývaly kusy grafu.
- S logaritmickým měřítkem nakládejte opatrně. Při logaritmickém měřítku osy y se
vám z \(\log(n)\) stane \(\log\log(n) \), což může být těžké rozlišit od \( \log(n)
\), tj. původního \(n\), či od konstanty.
Nový úkol: ab_tree
- Implementujte insert v (a,b)-stromu.
- Má to háček: V úkolu je verze (a,b)-stromů s hodnotami i ve vnitřních vrcholech.
- Rozdíl oproti verzi s klíči jen v listech je malý, v podstatě je jen třeba při
štěpení poctivě migrovat hodnoty/klíče mezi vrcholy a nestačí jen kopírovat.
- Prosím nastudujte si změny ze skriptíček, kapitola 3.1. Vypadá to
dlouze, ale většinu věcí už jste viděli na přednášce (a pokud ne, tak je rozhodně
dobrý nápad si je nastudovat).
- V templatu je speciálně deklarovaná metoda
split_node. Pro tento
úkol není nijak důležitá, testy jí nekontrolují a pokud jí nepoužijete (smažete, ...),
nijak to vaše řešení neovlivní. ALE! Bude důležitá v dalším experimentálním úkolu, kde
se skrze ní počítá, ke kolika rozdělením vrcholů došlo (podobně, jako se u experimentu
na splay počítají rotace).
Př. 0: (a,b)-strom s hodnotami ve vnitřních vrcholech
Nastudujte si insert a delete v (a,b)-stromech s hodnotami ve vnitřních vrcholech ze
skriptíček.
Př. 1: Insert a delete
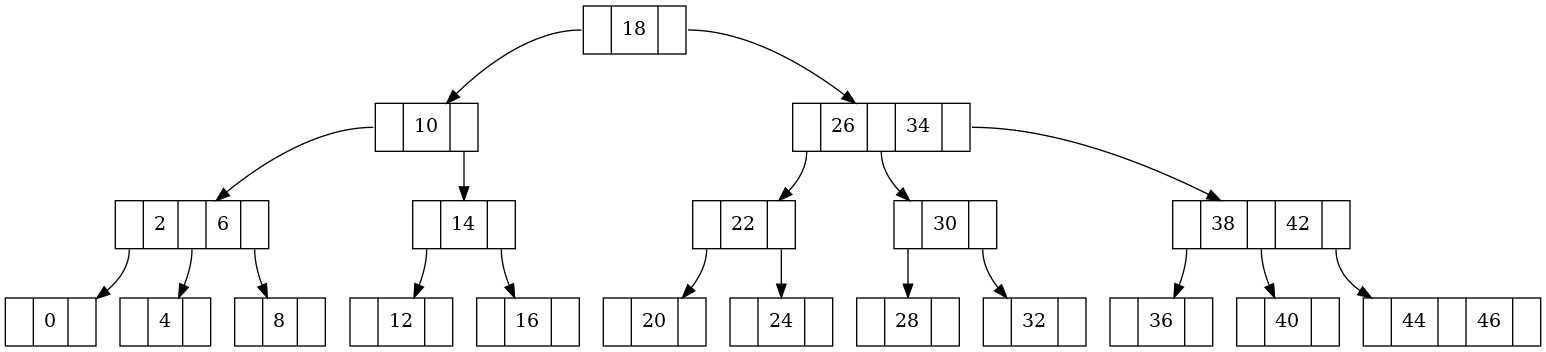
Na (2,3)-stromu z obrázku proveďte operace dané níže. Každou operaci proveď zvlášť,
začínaje vždy znovu se stromem z obrázku. Strom má hodnoty i ve vnitřních vrcholech.
- Insert 7
- Insert 48
- Delete 44
- Delete 40
- Delete 32
- Delete 30
- Delete 16
Řešení si můžete zkontrolovat pomocí vizualizace,
strom z obrázku vznikne vložením těchto hodnot (přesně v tomto pořadí):
28, 24, 26, 18, 0, 36, 16, 34, 22, 10, 2, 30, 4, 6, 20, 12, 32, 38, 14, 8, 40, 42, 44, 46
Vizualizace podporuje jen \((\lceil b/2 \rceil,b)\)-stromy.
